Research Topics
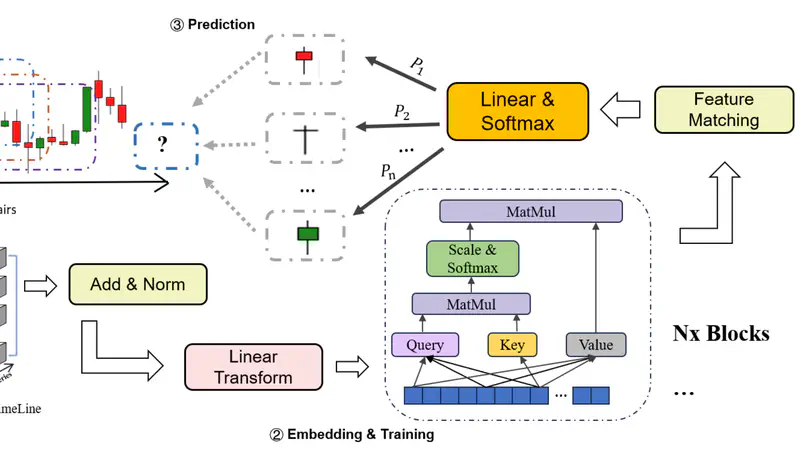
Deep learning has emerged as a powerful tool for analyzing high-frequency financial data, offering sophisticated capabilities to capture complex patterns and nonlinear relationships in market dynamics. These advanced models, particularly those based on Transformer networks, recurrent neural networks (RNNs), and long short-term memory (LSTM) networks, can process massive amounts of time-series data to predict market movements, assess volatility, and automate trading decisions with remarkable precision.
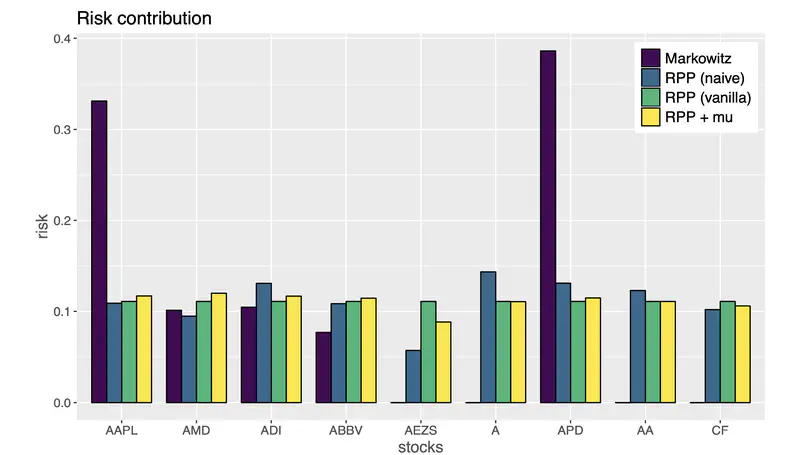
Portfolio optimization stands as a cornerstone of modern investment management, focusing on the systematic selection of optimal asset allocations that balance expected returns against financial risk. Since Harry Markowitz’s groundbreaking 1952 paper on Portfolio Selection, for which he later received the Nobel Prize in Economic Sciences, the field has evolved significantly beyond the traditional mean-variance framework.
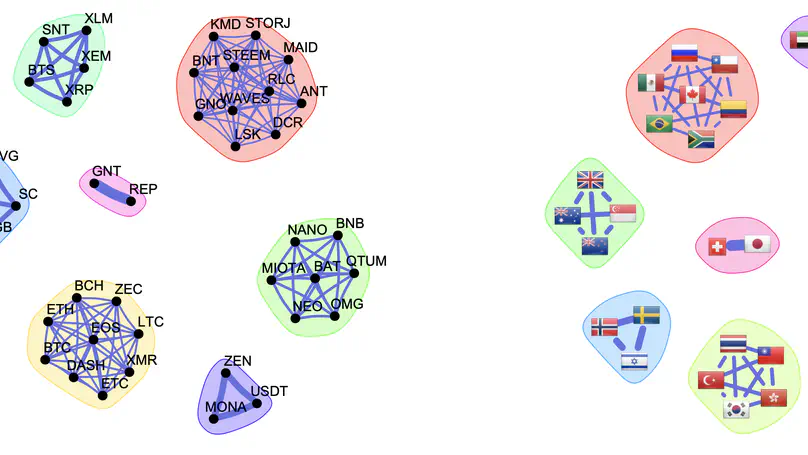
Financial markets are inherently interconnected systems where assets, institutions, and market participants form complex networks of relationships that evolve over time. Graph learning has emerged as a powerful framework for understanding and modeling these financial networks, enabling the discovery of meaningful relationships among stocks, cryptocurrencies, or other financial instruments through their return time series, trading volumes, or other market indicators.

Traditional convex optimization methods and signal processing techniques can be employed in big data problems characterized by large amounts of data in high-dimensional spaces. However, big data brings additional difficulties that need to be taken care of such as high-computational cost that require simple and efficient methods, distributed implementations, faulty data in the form of outliers, etc.
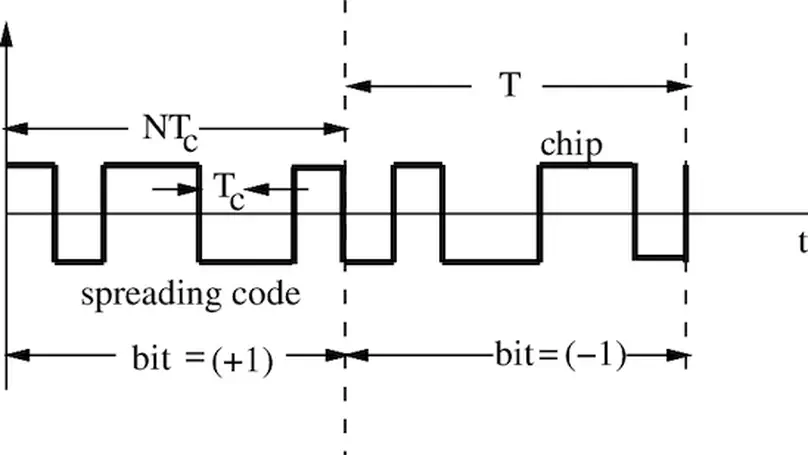
Carefully designed sequences lie at the heart of virtually any digital system commonly used in our daily lives. Examples include GPS synchronization, multiuser CDMA systems, radar ambiguity function shaping, cryptography for secure transactions, and even the watermarking of digital images or videos.
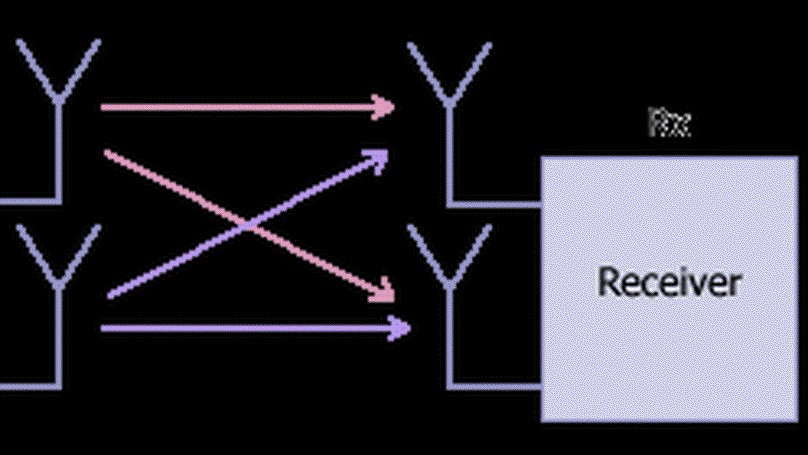
Multiple-input multiple-output (MIMO) channels provide an abstract and unified representation of different physical communication systems, ranging from multi-antenna wireless channels to wireless digital subscriber line systems. They have the key property that several data streams can be simultaneously established.

The Variation Inequality (VI) problem constitutes a very general class of problems in nonlinear analysis. The VI framework embraces many different types of problems such as systems of equations, optimization problems, equilibrium programming, complementary problems, saddle-point problems, Nash equilibrium problems, and generalized Nash equilibrium problems.

Radio regulatory bodies are recently recognizing that rigid spectrum assignment granting exclusive use to licensed services is highly inefficient. A more efficient way to utilize the scarce spectrum resources is with a dynamic spectrum access, depending on the real spectrum usage and traffic demands.
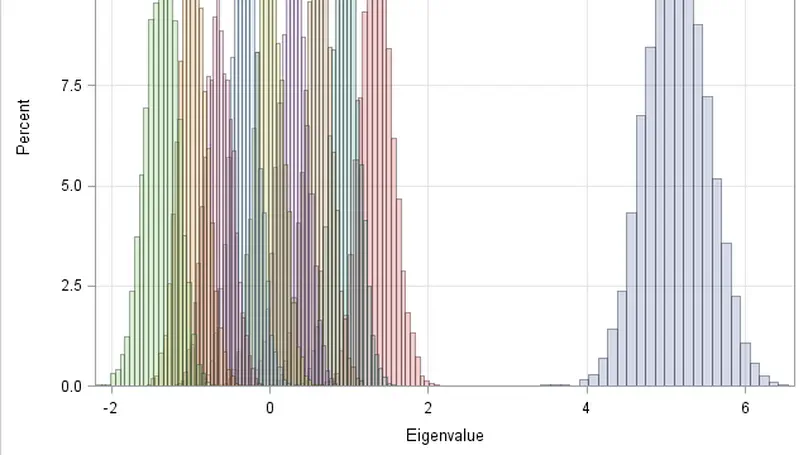
The performance of multiple-input multiple-output (MIMO) communication systems is related to the eigenstructure of the channel matrix H (channel eigenmodes) or, more exactly, to the non-zero eigenvalues of HH†. Therefore, the probabilistic characterization of these eigenvalues is necessary in order to derive analytical expressions for the average and outage performance measures of the system.